Windows executable (command line tool!), linux (x64) executable and source code (for C++/Python) are available from SourceForge.

If you find a bug, request a feature or need support open a ticket or discuss it in the SourceForge pages.

In portfolio theory agents attempts to maximise portfolio expected return for a given amount of portfolio risk, or equivalently to minimise risk for a given level of expected return.

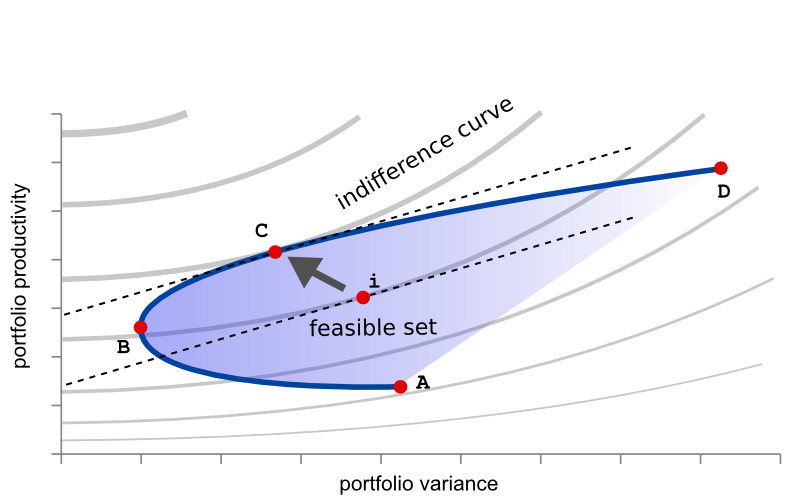
The portfolio management can be portrayed graphically as in the above Figure, where the feasible set of variance-profitability combinations in enclosed by the blue curve and the B-D segment represents the efficient frontier, where no variance can be lowered at productivity's price or equivalently no productivity can be increased at price of increasing variance.

In order to simplify computations, forest managers are assumed to have risk aversion with simple linear preferences, that is they are willing to trade off variance with productivity proportionally. In such case the indifference curves can be drawn like a bundle of straight lines having equation $prod = \alpha * var + \beta$, where $\alpha$ is the linear risk aversion coefficient and both $prod$ and $var$ refer to the overall portfolio's productivity and variance.

Point $B$ represents the point having the lowest possible portfolio variance. Agents with $\alpha$ risk aversion will choose however the tangent point $C$ that can be obtained by solving the following quadratic problem:

\begin{equation} \begin{array}{rrrll} \max_{x_i, \beta} & Y & = & \beta & \\ s.t. & & & & \\ & x_i & \geqslant & 0 & \forall i\\ & \sum_i x_i & = & 1 & \\ & \sum_i {x_i p_i} & = & \alpha \sum_i { \sum_j { x_i x_j \sigma_{i,j}}} + \beta & \\ \end{array} \label{eq:optimisation_problem1} \end{equation}

that by substitution become:

\begin{equation} \begin{array}{rrrll} \min_{x_i} & Y & = & \alpha \sum_i { \sum_j { x_i x_j \sigma_{i,j}}} - \sum_i {x_i p_i} & \\ s.t. & & & & \\ & x_i & \geqslant & 0 & \forall i\\ & \sum_i x_i & = & 1 & \\ \end{array} \label{eq:optimisation_problem2} \end{equation}

where $x_i$ is the share of the asset $i$, $p_i$ is its productivity, $\sigma_{i,j}$ is the covariance between assets $i$ and $j$ and hence $\sum_i {x_i p_i}$ is the overall portfolio productivity and $\sum_i { \sum_j { x_i x_j \sigma_{i,j}}}$ is its variance.

As the only quadratic term arises when $i=j$ and $\sigma_{i,j}$ being the variance is always positive, the problem is convex and hence easily numerically solved.

g++ -std=c++0x -O -o portopt_executable QuadProg++.cpp Array.cpp anyoption.cpp portopt.cpp  main.cpp 

g++ -fPIC -std=c++0x -O -c QuadProg++.cpp Array.cpp anyoption.cpp portopt.cpp main.cpp 
g++ -std=c++0x -O -shared -Wl,-soname,portopt.so -o portopt.so QuadProg++.o Array.o anyoption.o portopt.o

Then link your program e.g. with:

g++ -std=c++0x -O -o portopt_executable main.o -Wl,-rpath,'$ORIGIN' -L . portopt.so
./portopt_executable

swig -c++ -python portopt.i
g++ -fPIC -std=c++0x -O -c QuadProg++.cpp Array.cpp anyoption.cpp portopt.cpp portopt_wrap.cxx main.cpp -I/usr/include/python2.7 -I/usr/lib/python2.7
g++ -std=c++0x -O -shared -Wl,-soname,_portopt.so -o _portopt.so QuadProg++.o Array.o anyoption.o portopt.o portopt_wrap.o

(then please refer to the python example for usage)

If you want to change the output library name (e.g. you want to create _portopt_p3.so for python3 alongside _portopt.so for python2), do it in the %module variable of portopt.i and in the -soname and -o options of the linking command (and don't forget to use the right python included directory in the compilation command).
You can then load the correct module in your script with something like:

import sys
if sys.version_info < (3, 0):
  import portopt
else:
  import portopt_p3 as portopt

Please notice that the API changed from version 1.1, with the introduction of the port_opt_mean and port_opt_var parameters (both by reference). For the old 1.1 call instructions see here.

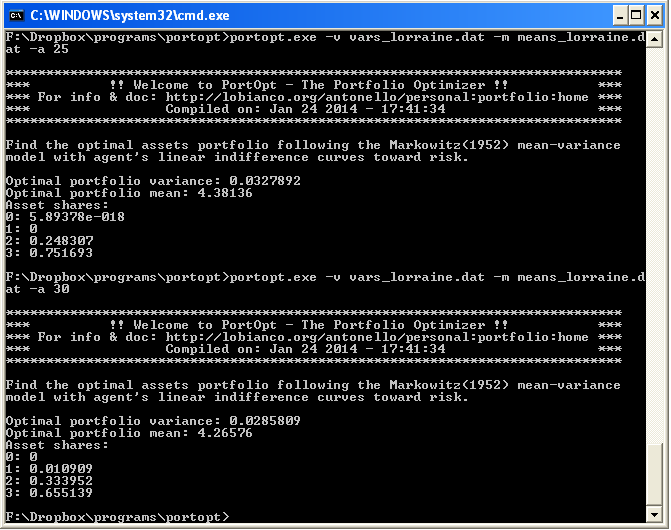
./portopt [options]

portopt.exe [options]

(from a DOS prompt: (a) START→run→“cmd”; (b) cd \path\to\portopt )

Call:

double solveport (const vector< vector <double> > &VAR, const vector<double> &MEANS, const double &alpha, vector<double> &x_h, int &errorcode, string &errormessage, double &port_opt_mean, double &port_opt_var, const double tollerance = 0.000001)

import portopt
results = portopt.solveport(var,means,alpha,tolerance) # tolerance is optional, default to 0.000001
functioncost = results[0]
shares       = results[1]
errorcode    = results[2]
errormessage = results[3]
opt_mean     = results[4]
opt_var      = results[5]

  -h  --help                                   Prints this help 
  -v  --var-file [input_var_file_name]         Input file containing the variance/covariance matrix (relative path)   
  -m  --means-file [input_means_file_name]     Input file containing the means vector (relative path)  
  -a  --alpha [alpha_coefficient]              Coefficient between production and risk in the linear indifference curves   
  -f  --field-delimiter [field_delimiter]      Character to use as field delimiter (default: ';')  
  -s  --decimal-separator [decimal-separator]  Character to use as decimal delimiter (default: '.')
  -t  --tollerance [tolerance]                 A tolerance level to distinguish from zero (default: 0.000001) 

• Higher the alpha, lower the agent risk aversion;
• Set a negative alpha to retrieve the portfolio with the lowest possible variance;
• Set alpha to zero to retrieve the portfolio with the highest mean, independently from variance (solution not guaranteed to be unique);
• Assets shares are returned in the x_h vector, eventual error code (0: all fine, 1: input data error, 2: no solutions, 3: didn't solve, 4: solver internal error) in the errorcode parameter.
• Use option “tollerance” with two l up to version 1.1 included

Copyright (C) 2014 Antonello Lobianco.

PortOpt is free software: you can redistribute it and/or modify it under the terms of the GNU Lesser General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

PortOpt is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU Lesser General Public License along with PortOpt. If not, see http://www.gnu.org/licenses.

If you use this program or a derivative of it in an academic framework, please cite it!
Please cite as:

• A. Dragicevic, A. Lobianco, A. Leblois (2016), “Forest planning and productivity-risk trade-off through the Markowitz mean-variance model”, Forest Policy and Economics, Volume 64, March 2016, Pages 25–34.

This work was supported by:

• a grant overseen by Office National des Forêts through the Forêts pour Demain International Teaching and Research Chair;
• the French National Research Agency through the Laboratory of Excellence ARBRE, a part of the “Investissements d'Avenir” Program (ANR 11 – LABX-0002-01).